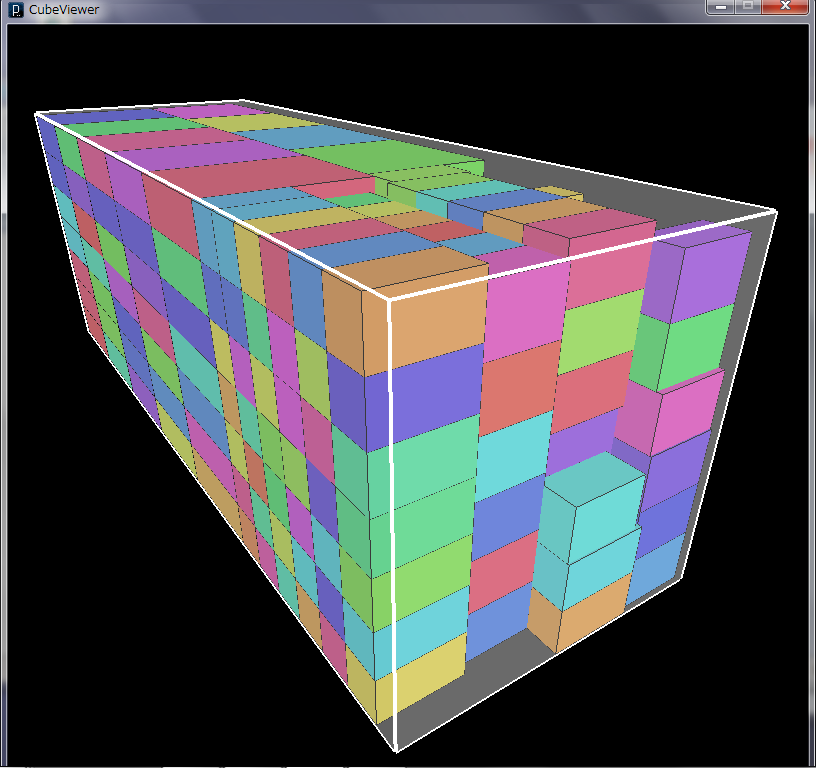
たとえば, さまざまな形の箱をできるだけ隙間なくコンテナに詰め込む, 看護師の要望をできるだけ反映した勤務表を作成する, 宅配便の効率的な配送計画を行うなど, 解決すべき組合せ最適化問題は世の中に無数に存在します. 以下に直方体の箱をコンテナに詰め込んだ一例を示します.

このように形状をできるだけ隙間なく詰め込むという問題は, 2次元や3次元のさまざまな形状に対して研究されており, 倉庫やトラック等に物をなるべくたくさん詰め込むというような 効率よい詰め込みを求める応用の他に, 大きな布から洋服の部品を切り出したり, 大きな鉄板から船や自動車等の製品の部品を切出し, 製品にならない無駄な部分をできるだけ少なくするというような応用もあります. 2次元の例として, ズボンの部品を切り出すレイアウト, シャツの部品を切り出すレイアウトの例と, レクトリニア図形すなわち縦横の線のみからなる図形を詰め込む レイアウトの例を紹介しておきます.

最適化の対象は効率化だけではありません. 夏休みに片道切符1枚でどれだけ長く鉄道旅行できるかを考えるのも, 最適化問題のひとつです.
このような問題をコンピュータを用いて解くには, 問題を解くための手続きを設計する必要があります. そのような手続きのことをアルゴリズムと呼びます. 出発地から目的地までの最短のルートを求める問題には 効率の良いアルゴリズムがあり,カーナビなどに応用されています. しかし,「いくつかのお店で買い物をして自宅に帰るまでの最短のルートを求める」 という問題は,一見最初の問題に似ているように思えるにもかかわらず, 難しいことが知られています. 問題の難しさを解明したり, 効率の良いアルゴリズムを開発するのが主要な研究テーマです.
身近な現実問題を解決するソフトウェアの開発にも力を入れています. たとえば京都大学数理解析研究所(RIMS)では,毎年数十件の研究集会が 開催されています.それらの日程と開催場所のスケジューリングは, これまで人手で行われており,かなりの時間を要していましたが, この作業を支援するソフトウェアを作成しました. このソフトウェアは現在RIMSの共同利用掛で利用されています. また,電気系の学生実験において学生を実験テーマに割り当てる作業など, 先生方がこれまで人手で行われていた大変な作業を自動化するソフトウェア を作りました.こちらも実際に学生実験の運営に利用されています.
アルゴリズムの開発には主にメタ戦略 と呼ばれる手法を使っています. 多くの現実問題を解決できる便利なアルゴリズムを作りたいと思っています.
以下は私たちの研究グループ(最適化アルゴリズムグループ)の研究成果を 分かりやすく紹介したビデオですので,ぜひご覧ください.
以下の情報もぜひご覧ください.